Извините, этот техт доступен только в “Беларуская” и “Американский Английский”. For the sake of viewer convenience, the content is shown below in this site default language. You may click one of the links to switch the site language to another available language.

Сэрвіс “Графічнае адлюстраванне контуру асноўнага тону” дазваляе карыстальніку атрымаць графічнае адлюстраванне контуру асноўнага тону маўленчай фразы анлайн. На ўваход сэрвісу даецца фанаграма фразы працягласцю не больш за хвіліну. Фанаграма можа быць загружана на сэрвіс з цвёрдага дыску камп’ютара або па спасылцы з сеткі Інтэрнэт, павінна быць у фармаце .wav ці запісана праз магчымасці аўдыязапісу сэрвісу. На выхадзе атрымліваюцца малюнкі асцылаграмы, спектраграмы і контура асноўнага тону запампаванай фразы.

Асноўныя тэрміны і паняцці

Частата асноўнага тону (ЧАТ) з’яўляецца адным з важнейшых фізічных параметраў маўленчага сігналу. З пункту гледжання акустыкі яна ўяўляе сабой першую гармоніку танальнага складніка сігналу, які зазвычай нясе максімальную энергію. Наяўнасць частаты асноўнага тону ўласцівая вакалізаваным гукам (усім галосным і частцы зычных, напрыклад, звонкім), і наадварот, яе адсутнасць уласцівая глухім зычным. Дынаміка контуру ЧАТ мае прамую карэляцыйную сувязь з прасадычнымі характарыстыкамі маўлення, такімі як:

• мелодыка (рух частаты асноўнага тону);
• рытміка (бягучая змена працягласці гукаў і паўз);
• энергетыка (бягучае змяненне сілы гука).

Практычная каштоўнасць

Дакладная ідэнтыфікацыя і аналіз гэтых параметраў з’яўляецца важным этапам у даследаваннях спецыялістамі (фанетыстамі, фонаскапістамі і інш.) гутарковага маўлення з мэтай вызначэння розных прасадычных і інтанацыйных з’яў вуснага маўлення. Сэрвіс можа выкарыстоўвацца ў праграмах для вывучэння інтанацый замежных моў, аплікацый фанаскапічнай экспертызы.

Асаблівасці сэрвісу

Сэрвіс выкарыстоўвае перцэптыўны алгарытм вылічэння ЧАТ – SWIPE [1], заснаваны на аўдыторнай мадэлі ўспрымання ЧАТ чалавекам. Дадзены алгарытм з’яўляецца адным з самых якасных і распаўсюджаных алгарытмаў вызначэння ЧАТ на сённяшні дзень [2].

Апісанне інтэрфейсу карыстальніка

Графічны інтэрфейс сэрвісу ўключае наступныя асноўныя часткі, прадстаўленыя на малюнку 1.

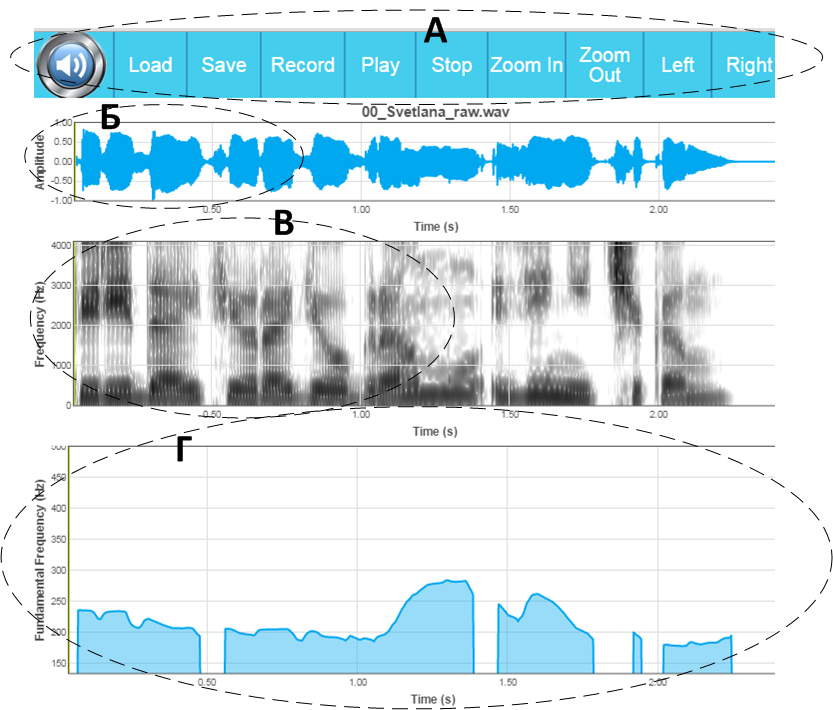Малюнак 1 – Графічны інтэрфейс сэрвісу

Каманднае меню (A) змяшчае наступныя пункты:

• • Load (Загрузіць) – загрузіць аўдыяфайл з лакальнага дыску камп’ютара ці з іншага месца па URL (аўдыяфайл абавязкова павінен быць у фармаце WAV).
  • Save (Захаваць) – захаваць аўдыяфайл (ці яго фрагмент) на лакальны дыск камп’ютара карыстальніка.
  • Record (Запісаць) – пачаць запіс з мікрафона, калі ён ёсць і падключаны да камп’ютара карыстальніка.
  • Play (Прайграць) – праслухаць аўдыяфайл ці яго частку (у залежнасці ад таго, увесь файл ці толькі яго фрагмент у дадзены момант адлюстроўваецца і апрацоўваецца ў акне асцылаграмы. Больш падрабязна праца з фрагментам будзе апісана далей).
  • Stop (Прыпыніць) – прыпыніць праслухоўванне аўдыяфайла.
  • Zoom In (Павялічыць) – павялічыць фрагмент файла, выдзелены з дапамогай маркераў левай і правай мяжы фрагменту. Маркер левай мяжы мае зялёны колер і можа быць выстаўлены клікам левай кнопкі мышкі ў акне асцылаграмы. Маркер правай мяжы мае чырвоны колер і можа быць выстаўлены клікам правай кнопкі мышы ў акне асцылаграмы. Больш падрабязнае апісанне будзе прыведзена далей.
  • Zoom Out (Паменшыць) – паменшыць фрагмент файла, вярнуцца да прагляду ўсяго файла цалкам.
  • Left (Улева) – змясціць файл на адно акно ўлева.
  • Right (Управа) – змясціць файл на адно акно ўправа.

Асцылаграма сігналу (Б) – двухмернае часавае адлюстраванне сігналу. Больш дакладна, гэта залежнасць амплітуды сігналу ад часу: вось абсцыс (х) – час, вось ардынат (y) – амплітуда сігналу. На гэтым графіку добра бачна дынаміка энергіі сігналу і змяненне магутнасці ўсіх яго кампанентаў разам (танальнай, шумавой).

Спектраграма сігналу (В) – трохмернае частотна-часавае адлюстраванне сігналу. Больш дакладна, гэта залежнасць магутнасці сігналу ад часу і частаты адначасова: вось абсцыс (х) – час, вось ардынат (y) – частата, вось аплікат (z) – магутнасць сігналу (у дадзеным выпадку замест асобнай графічнай восі выкарыстоўваецца колер: чым большая інтэнсіўнасць колеру, тым большую магутнасць мае сігнал на гэтай частаце ў дадзены момант часу). У адрозненні ад асцылаграмы, спектраграма дазваляе ўбачыць асобны ўнёсак кампанентаў сігналу, якія маюць найбольшую энергію ў канкрэтны момант часу (танальныя ці шумавыя кампаненты, якія гармонікі паасобку і г.д.).

Графік контуру частаты асноўнага тону (Г) – двухмернае адлюстраванне эвалюцыі значэння ЧАТ у залежнасці ад часу. Вось абсцыс (х) – час, вось ардынат (у) – частата (Гц). Адсутнасць азначае невакалізаваны фрагмент маўлення (напрыклад, глухія зычныя: к, х, ч, ш, т, с, ф).

Карыстальніцкія сцэнары працы з сэрвісам

Сцэнар 1. Адлюстраванне контуру ЧАТ аўдыяфайла, захаванага на лакальным дыску камп’ютара

1.1. Зайсці на старонку сэрвісу “Графічнае адлюстраванне частаты асноўнага тону”.

1.2. Націснуць кнопку Load.

1.3-а. У акне выбару файла націснуць “Выбраць файл”. Адкрыецца стандартнае дыялогавае акно аперацыйнай сістэмы для выбару файла на дыску. Выбраць файл з лакальнага дыску камп’ютара.

1.3-б. У акне ўвесці URL да файла, які знаходзіцца ў сетцы, напрыклад: http://corpus.by/tts3/cache/out/2015-11-26_21-39-53_134-17-130-18_931_bel_ssrlab.wav

1.4. Дачакацца адлюстравання асцылаграмы, разліку спектраграмы і контуру ЧАТ (малюнак 2).

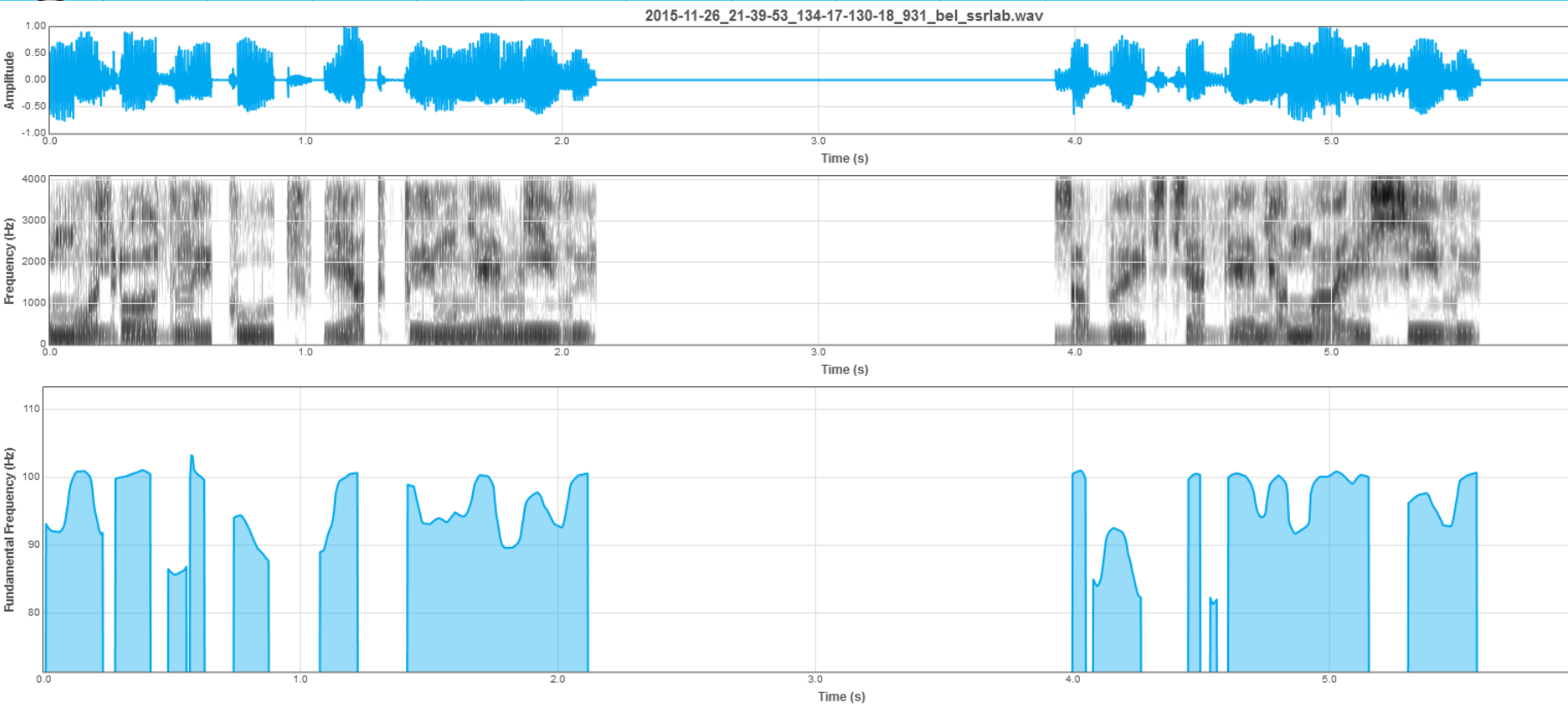Малюнак 2 – Адлюстраванне асцылаграмы, спектраграмы і контуру ЧАТ

Сцэнар 2. Адлюстраванне контуру ЧАТ аўдыяфайла, запісанага з мікрафону

2.1. Упэўніцца, што ў вас падключаны і працуе мікрафон.

2.2. Зайсці на старонку сэрвісу “Графічнае адлюстраванне частаты асноўнага тону”.

2.3. Націснуць кнопку Record.

2.4. Пагадзіцца з прапановай браўзера весці гуказапіс.

2.5. Запісаць фразу ці некалькі фраз, назіраючы выніковы сігнал у акне асцылаграмы ў рэальным часе.

2.6. Націснуць кнопку Stop для заканчэння запісу і адлюстравання вынікаў.

2.7. Пры неабходнасці захавання фразы на камп’ютары націснуць кнопку Save.

Сцэнар 3. Праца з часткай аўдыяфайла

3.1. Выканаць усе пункты сцэнару 1 або сцэнару 2 па выбары карыстальніка.

3.2. Паставіць маркер левай мяжы фрагменту. Для гэтага навесці мышку на любую з абласцей і націснуць левую клавішу. Павінна з’явіцца зялёная лінія – левай мяжа фрагменту (малюнак 3).

3.3. Паставіць маркер правай мяжы фрагменту. Для гэтага навесці мышку на любую з абласцей правей за левую мяжу і націснуць правую клавішу. Павінна з’явіцца чырвоная лінія – правая мяжа фрагменту (малюнак 3).

Малюнак 3 – Маркеры левай і правай межаў фрагмента

3.4. Націснуць клавішу Zoom In для павелічэння маштабу выбранага фрагменту сігналу (малюнак 4).

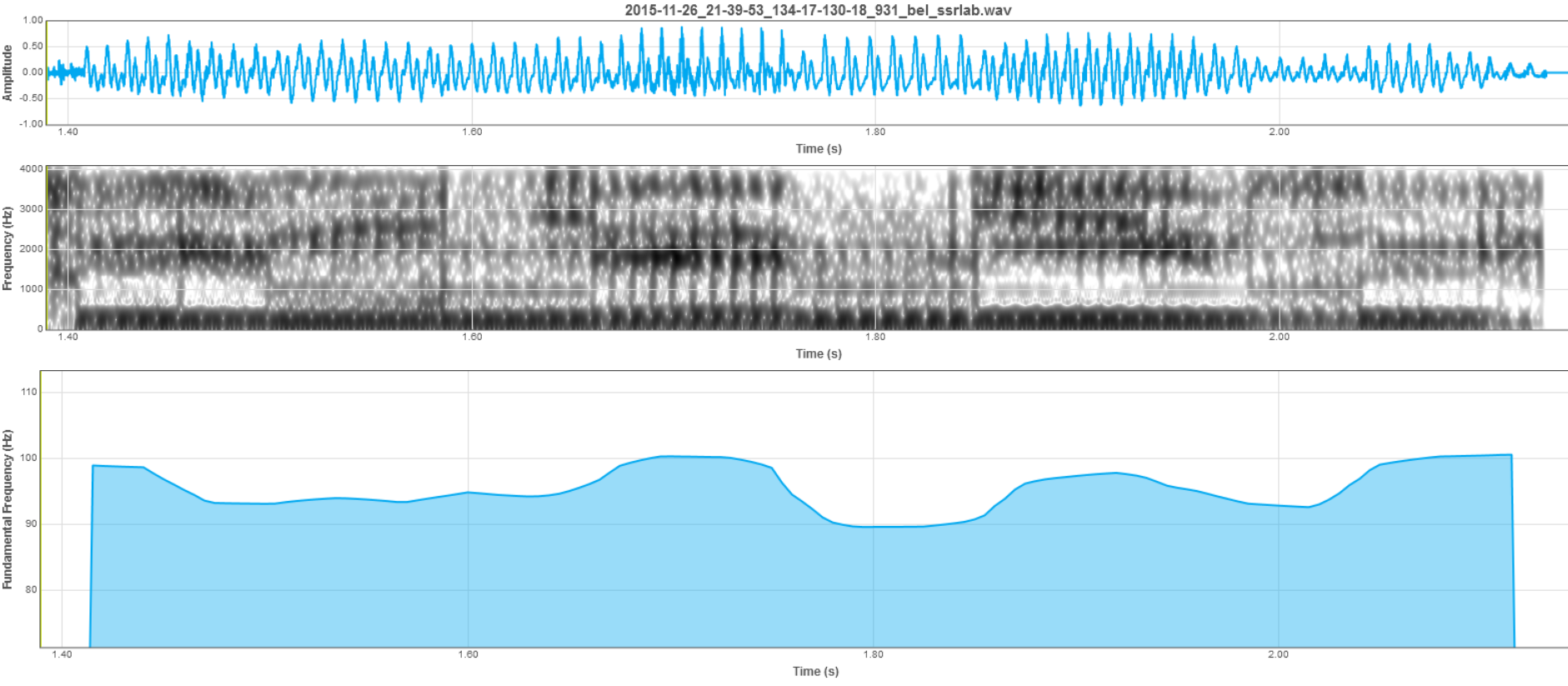Малюнак 4 – Павялічаны фрагмент

3.5. У такім рэжыме ёсць магчымасць карыстацца функцыямі агучвання і захавання сігналу ў кантэксце дадзенага фрагменту. Гэта значыць, што будзе прайгравацца і захоўвацца толькі выбраны фрагмент сігналу.

3.6. Пры неабходнасці большага павелічэння маштабу трэба паўтарыць крокі 3.2-3.5.

3.7. Для вяртання назад да папярэдняга маштабу трэба націснуць Zoom Out.

3.8. У рэжыме павелічэння маштабу пры націсканні кнопак Left і Right адбываецца змяшчэнне бягучага фрагменту сігналу на адзін фрагмент (экран) у левы бок, ці на адзін фрагмент (экран) у правы бок па часавай восі.

Мадэль, алгарытм

З матэматычнага пункту гледжання працэс апрацоўкі інфармацыі ў сэрвісе “Графічнае адлюстраванне контуру асноўнага тону (Pitch Plotter)” можна прадставіць з дапамогай наступнага выразу:

\[\left(\ \textbf{o,S,p}\ \ \right)={\mathcal P}\left(\textbf{x}\right),\]

дзе $\textbf{x}=\left\{x\left(n\right)\ |\ x\in R,\ n=\overline{0,1,2,\dots ,N-1}\right\}\ $ – вектар адлікаў уваходнага маўленчага сігналу. Сігнал быў атрыманы з wav-файла, запампаванага ў сэрвіс пры дапамозе каманды “Load”, або з мікрафона карыстальніка пры дапамозе каманды “Record”, $n$ – нумар адліку ў сігнале.

дзе $\textbf{o}=\left\{o\left(n\right)\ |\ o\in R,\ n=\overline{0,1,2,\dots ,N-1}\right\}\ $ – асцылаграма сігналу (вектар значэнняў кропак графіка асцылаграмы), $n$ – нумар адліку ў сігнале.

дзе $\textbf{S}=\left\{s\left(k,m\right)\ |\ s\in R,\ m=\overline{0,1,2,\dots ,M-1},\ k=\overline{0,1,2,\dots ,K-1}\ \right\} $ – спектраграма сігналу (матрыца значэнняў кропак графіку спектраграмы), $k$ – нумар гармонікі сігналу, $m$ – нумар фрэйму сігналу.

дзе $\textbf{p}=\left\{p\left(m\right)\ |\ p\in R,\ m=\overline{0,1,2,\dots ,M-1}\right\} $ – графік частаты асноўнага тону (вектар значэнняў кропак графіка), $m$ – нумар фрэйму сігналу.

Такім чынам, можна сцвярджаць, што функцыя ${\mathcal P}$, якая апісвае працу сэрвісу, складаецца з суперпазіцыі трох пераўтварэнняў:

\[\left\{ \begin{array}{c}
\textbf{x}\ {{\stackrel{{{\mathcal P}}_o}{\longrightarrow}\ \textbf{o}}}, \\
\textbf{x}\ {{\stackrel{{{\mathcal P}}_s}{\longrightarrow}\ \textbf{S}}}, \\
\textbf{(x,S)}\ {{\stackrel{{{\mathcal P}}_{x,S}}{\longrightarrow}\ \textbf{p}}} \end{array}
\right\}\]

Разгледзім больш падрабязна кожнае з іх:

1. Для атрымання асцылаграмы сігналу не патрэбна выкананне ніякіх пераўтварэнняў уваходных дадзеных, атрыманыя адлікі адразу могуць быць адлюстраваныя. Такім чынам, функцыя ${{\mathcal P}}_o$ выглядае як:

\[\textbf{o}={{\mathcal P}}_o\left(\textbf{x}\right)\Longrightarrow \textbf{o}\left(n\right)=1\cdot x\left(n\right)\Longrightarrow \textbf{o}\Longleftrightarrow \textbf{x}.\]

2. Для атрымання ${{\mathcal P}}_s$ і ${{\mathcal P}}_p$ выкарыстоўваецца дыскрэтнае пераўтварэнне Фур’е (ДПФ), якое разгледзім больш падрабязна. ДПФ дазваляе перайсці з часовай у частотную вобласці, дзе лепш бачныя асобныя складнікі сігналу (гармонікі) і можна прасцей зрабіць яго аналіз (малюнак 5.1).

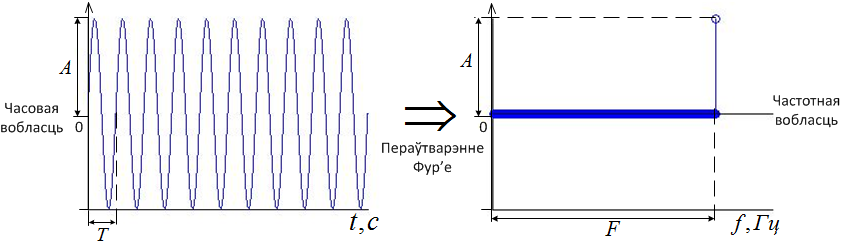
Малюнак 5.1 – Пераход з часовай у частотную вобласці

Запішам формулу пераўтварэння Фур’е:

\[X\left(f\right)={\mathcal F}\left(x\left(t\right)\right)=\int^{+\infty \ }_{-\infty \ }{x\left(t\right)\cdot e^{-jwt}dt,} \\ – \infty < t <+\infty,- \infty< f <+ \infty\ \]

Пяройдзем да дыскрэтнага выгляду пераўтварэння, выканаўшы дыскрэтызацыю бесперапынных велічынь часу і частаты:

\[t=n\cdot T_s,\ ~n=\overline{0,1,\dots ,N-1}\ \]

\[f=k\cdot F_1,\ ~k=\overline{0,1,\dots ,K-1}\]

дзе $T_s$ – перыяд дыскрэтызацыі сігналу, $F_1$ – частата першай гармонікі сігналу. Тады пераўтварэнне Фур’е ў дыскрэтным выглядзе будзе:

\[X[k]={\mathcal F}\left(x[n]\right)=\sum^N_{n=1}{x[n]\cdot e^{-j2\pi (k\cdot F_1)(n\cdot T_s)}}\]

Можна прадставіць гэты выраз у матрычным выглядзе як:

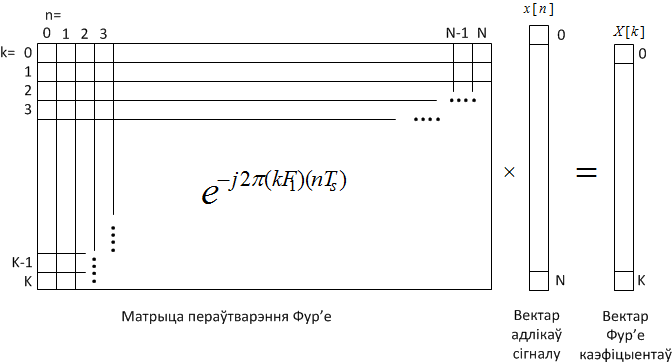
Малюнак 5.2 – Пераўтварэнне Фур’е ў матрычным выглядзе

Паколькі ядро пераўтварэння $e^{-jwt}$ Фур’е мае камплексны выгляд, для лепшага разумення фізічнага сэнсу распішам гарманічныя функцыі ў сапраўдным выглядзе з дапамогай пераўтварэння Эйлера, якое мае наступны выгляд:

\[e^{-j\varphi }=cos\varphi -jsin\varphi \]

\[X[k]={\mathcal F}\left(x[n]\right)=\sum^N_{n=1}{x[n]\cdot (cos⁡(2\pi kF_1nT_s)-jsin(2\pi kF_1nT_s))}\]

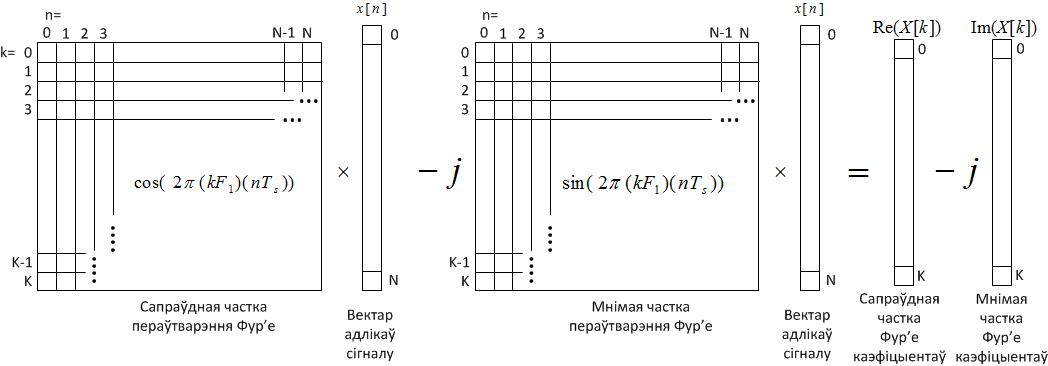
Малюнак 5.3 – Гарманічныя функцыі ў сапраўдным выглядзе, распісаныя з дапамогай пераўтварэння Эйлера

Для атрымання спектраграмы пераўтварэнне Фур’е выконваецца для кожнага $m$-га фрэйму $r$ сігналу:

Фрэйм $r$ – гэта адрэзак сігналу даўжынёй $L$ адлікаў, які ў апрацоўцы сігналаў называюць фрэймам.

\[r_m=\{x\left[l\right],\ ~l=\overline{m\cdot t,m\cdot t+1\dots m\cdot t+L}\ ,\ m=\overline{0,\ \dots ,M}\ \ \},\]

дзе $l$ – нумар адліку сігналу ўнутры фрэйму, $m$ – нумар фрэйму, $t$ – крок аналізу сігналу, $L$ – працягласць фрэйму ў адліках.

Такім чынам, функцыя ${{\mathcal P}}_S$ выглядае як:

\[\textbf{S}={{\mathcal P}}_S\left(\textbf{x}\right)\Longrightarrow S=abs({\mathcal F}(x\left[k,m\right])).\]

3. Для атрымання контуру асноўнага тону трэба выкарыстаць алгарытм ацэнкі SWIPE (a sawtooth waveform inspired pitch estimator). Ён выкарыстоўвае часавае і частотнае прадстаўленне сігналу. Працэдура, якая выконвае гэты алгарытм, з’яўляецца даволі складанай і таму разглядацца тут не будзе. Для зацікаўленых падрабязнае матэматычнае апісанне можна знайсці па спасылцы [1].

Такім чынам, функцыя ${{\mathcal P}}_{o,S}$ выглядае як:

\[\textbf{p}={{\mathcal P}}_{o,S}\left(\textbf{x,S}\right)=SWIPE(\textbf{x,S}).\]

Такім чынам, мы разглядзелі матэматычную мадэль сэрвісу Pitch Plotter.

Спасылкі на крыніцы

Відэаўрок па працы з гэтым сэрвісам: Pitch Plotter tutorial – Corpus.by

Старонка сэрвісу: http://corpus.by/PitchPlotter/?lang=be

Перакрыжаваныя спасылкі

1. SWIPE
2. Instantaneous Pitch Estimation based on Rapt Framework
3. Русак, В.П. Программная обработка фонетических особенностей белорусских говоров центрального региона / В.П. Русак, Ю.С. Гецевич // Исследования по славянской диалектологии 19–20. Славянские диалекты в современной языковой ситуации. Диалектный словарь как способ исследования славянских диалектов / отв. редактор выпуска: д. ф. н. Л. Э. Калнынь. — Москва : Институт славяноведения РАН, 2018. — C. 87-94.